Not much!

Got a few more jets and filled out my jetbox a bit more.
Useful addition to the dash, a 12V fag lighter outlet, like a fag lighter but without the lighter bit. Means I can charge and power stuff!
Lowered the front about 1/2".

Not driven it since the last blog entry. Just waiting for an excuse for a decent journey to go on / do some decent logging of a few jet changes. Also need to relocate my speedo's pickup, it's a bit random, I was going to check via GPS. 3000rpm in 4th should be 50mph.

Matrix Mode

Another useful logging method in which can display average AFR readings in each cell versus MAP and RPM, some have min of 10 logs per cell and other have up t0 600 or more, so a good average is made.

Image above is more open road slow cruise, hense leaner low down than the image below, but below is a different idle jet setup. The image below has some slow town work and some fast acceleration between, so more green rich readings lower down as slow speed acceleration was dominating and use of the pump jet, lots of pulling off junctions and using idle to 2500 to accelerate. Idle is best at 12.7-12.9 so this dominates at slow speed, once constantly rolling as above it leans off.

Found 7850.1 and 55 idle is now better than my 7850.9/58...I couldnt use 7850.1/55 before as the 5 tube was too delayed...I will testing my hunch as per the other two postings made once my 150 correctors arrive!

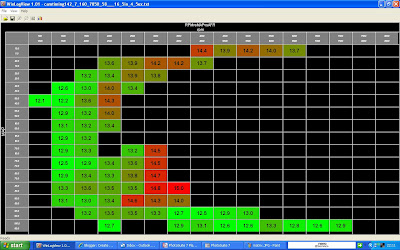
So it's important to take readings in context. You'd say it was too rich in the 2nd image, but when your not accelerating its ok as per the first one! or similar, can't be the same as the jetting is different!

Car has been giving me some postive payback lately. I like to make steps forward, clear improvements and developments. Its coming together nicely but the package needs polish in some areas. The rear suspension is miles better now it's lowered, even if the straight line traction is slightly impeeded by the extreme camber, or made the extra power?

Engine is running nicely, nice and smooth at the top you can batter the limiter in 2nd, 3rd and 4th and it feels happy. Cam timing is working well yet I am sure I can squeeze something more from it, but I want to work on this cross jetting before another stab.

Its a pleasure to drive like a granddad just pottering at 1000-2500 rpm...Runs nicely down there, will drive and pickup from 1000rpm in 5th, can slot it into 5th at 25mph, its quiet and smooth. Seems to be doing good gas mileage, excellent when really pottering. Good thing is, once the jetting is done it can only improve more when the ignition gets sorted! I don't think its far out though I worked on it some already.

Tuning detail

This is the about the last area requiring tuning. Marked in white dots. The image at the bottom of this post has red dots, these are showing the exact area of concern, this is just a couple of seconds of logging.

I gave the pump rods 4 turns of enrichment from where they were but have yet to test this, I didn't use the car today. The pump adjustment was related to another issue, not the one I will ramble about here.

Above shows a small issue.

This was climbing a gradual hill in 4th gear, the engine was not gaining rpm, as shown, actually just loosing rpm or just static speed. Torque is ok so I am not into the throttle too far. The MAP reading is not accurate, it is different to the reading in the ECU, it reads too high. I have two MAP sensors connected, the one connected to this software needs calibrating to match the ECU output. I don't need to do this atm. I will do this to finalise the ignition though I need to get logs on the MAP to work out the final load sites.

Anyway. I have pinpointed this area to a certain location on the throttle, rpm range.

It's when you should be accelerating (in the carbs mind) but you are not gaining rpm, lightish load, you are very gradually and slowly opening the throttle from a cruising or level situation, so the pumpjet is not active.

Basically I have a small gap between the idle/progression and main jet. This graph shows this perfectly on a creeping acceleration. This effects other areas but the effect is hard to see or less obvious.

So my current jetting is;

58idle jet
7850.9 idle holder (quite weak)
142 main jet
7 emulsion tube
155 air corrector

I need to very slightly enrich the 7850.9 idle holder at the top of it's range by filling in 1 of the 6 small air holes I think, I don't want a richer idle jet as the mix is good elsewhere and the airholes in the holder effect the top of the holders rpm range more than the bottom.

Also firstly test dropping the air corrector on the main jet stack to 150 and then use a 140 main jet. This will fire up the mains a tiny bit earlier using a smaller corrector, earlier in the throttle position/rpm.

I then hope that the high-end mix and the rest of the mixture on main jet stays as it was.

I will have dropped the main jet size and moved the main jet stack operation down slighly in the rpm range while taking the progression/idle upwards to meet it.

I will firstly test the 150 corrector using 140 and 142 main jet's and examine around 10mins of data on each rather than messing with the idle jet, as I have a nice setting on this...

Thats the great thing about logging this stuff, it's all there to examine, you just need to sit calmly and remember the drive and how the data relates to your feeling.

I know when I was taking this data shown in the image the engine was struggling when it got to 15.4AFR under load, this is fine at light cruise, but not when you are in a mild acceleration phase or bringing load onto the engine. Certainly 16.4 is way too lean.

I looked at the screen of the laptop at exactly this point cause the engine just started to hunt and faulter. I know it doesn't like 15:4+ under any real loading...

I had this happening just 3 times or so in two log sessions of 5mins each, but the underlying overlap issue is there all the time, just not enough to cause a faulter or hunt, just a touch marginal.

If I can sort this problem there will be a good torque increase in slow transitions in this rpm window, or this throttle position location, it's not related just to rpm but also TPS...It's a very small window like two-three hundred rpm and 5% on the throttle spindle opening.

If I just push the throttle a little harder the main jets come on as soon as the MAP reading hits 89 and the problem is gone I see this on a few logs, also the pump jet activates on firmer pedal usage.

The issue is on creeping slow throttle opening between 84 and 89MAP in the rpm range of 3000-3200 or so.

I know that on the 160 air corrector the main jet overlap on the same idle/idle holder is too late, this issue is present all the time, hense I am using a 155 :)

Using a 145 main and the 160 corrector, the main jet mixture once it's working is basically what I have on the 142-7-155, same all over, just a but late, so the 140-7-150 should keep the same mix and make it happen a tiny bit earlier!!

If not enough I will doctor the idle holders. I'd rather bring the main in earlier to be honest as it livens up the "drive", the active and eager main encourages you to gun the engine :)

Dropping the main jet size may not be bad thing if I can bring it in earlier as in some other areas I have a touch too much fuel just over this area I am trying to fix, the air corrector acts in two ways, effecting the start point of the main jet and the high end, the smaller corrector won't enrich the main jet much at lower rpm (where my issue is)....So maybe this is the "perfect" setting!?

So there is science to my suggestions.

You can see the same thing going on two blocks to the right of the dots, I just open the throttle the MAP goes up two-three points, a tiny bit, not enough to get any pump jet and AFR jumps from 13.6 which is ideal for the situation and hits 15.4, had I just opened the throttle a tiny bit more it would have stayed at 13.6 or enriched to 13.2 or so.

The area just before the red dots (to the left) is when I levelled the throttle to a cruise, the area in the reddots is when I just feathered it back on, so this area needs minor enrichment as I increase load. This not an area to use the pump jet really, too slow on the pedal, I have stiff pump springs to keep them quiet here!...I look at the pump jet as the last resort, this is a challenge for jetting!

This is really minor stuff now, just cleaning out the final few annoyancies.

I was delibrately feathering the TPS here to get this exact info!

General stuff

Been alot of wideband logging when using the car. Also cam timing trials.

I have pretty much found the sweet spot on the exhaust cam. I don't know what lift this relates to but it's simply using the vernier marks and swinging it slightly either way and assessing the engine's performance.

I know that advancing the exhaust cam, or giving it less lift at TDC, less overlap doesn't work at all at the top end, the engine is a dog, but it it does drive better at very low rpm and low throttle opening...I swang this around enough to know where is good or within 3deg at the crank anyway, I can percieve any changes by feel below this level. I have something to go on when I decide to get the car on the rollers and setup the ignition anyway...

I know advancing the inlet cam doesn't work from where I timed it. The top-end goes, as you might expect. Advancing the inlet cam means the opposite of the exhaust, more advance means it opens the valve earlier, more lift at TDC. This means also that the valve closes earlier, so top-end power is reduced as the fuel isn't "rammed in" at high rpm and you loose the ability to "ram" fuel and air in via the speed of the inlet flow, that last "cram" of gas into the cylinder. I have yet to conclude my tests here. I am currently running 3deg @ the crank more than I timed the cam at.

I do feel I have a good setting atm, a good spread or torque and power.

This was complemented on a private test track last night. I took the car to 7200rpm in 4th which is about 122mph I think, on my 3.89 diff. I didn't bother to hit 5th and carry on :) Car was still pulling pretty hard when the rev limiter took over it was accelerating well at this speed and should max out in 5th gear I think, somewhere around 150mph?

It's the best its been at the top-end, the mixture is also faultless from 5900-7300 holding a constant WOT mix of 12.7 air to fuel ratio. I have a funny mild lean out from 5400-5900 where the mixture goes to 13.3, which is ok but a tad lean for peak power. I have this mixture issue on all jetting and cam timings...I could use a stack of different trumpets to test, I could be getting some stand-off or flow pulse issues here?!

I also find that the cam timing has some effects on the overlap from carb circuit to circuit. I had it near perfect but it seems to be flowing a tad more with the current cam timing and needs some very minor adjustments. I am very close to cracking the jetting. However first I want to conclude my cam timing experiments so as to have a firmer idea of any jets I need to acquire. So it's balancing alot of factors.

I have tested lots of jets. I have increased the gas mileage alot by changing my jetting dramatically from where it was before I fitted the logging equipment.

Plenty has gone on, but I can be bothered to relay it cause most of it was not worthwhile. This is a totally unknown setup, unknown head, cams, exhaust, inlet manifold, carbs, etc. So I have to do the job of a major manufactoring company to get the results I want!

Lowered the rear-end back down to "dog with an itchy arse setting"...Tracking was all screwed after I raised it 1inch from where the tracking was setup! Rears been a bit nervous, also adjusted my old SPAX dampers on the back using a hammer.

This is the 2J1 wideband unit. Must say it's been faultess in a few hours of testing, good bit of kit! You can log of alot of data from it, EGT, MAP, TPS, RPM, VOLTS, Fuel pressure etc and log all this in software.

I will pickup the next caterham manifold I see on ebay and keep this for the future with an eye to making a 4-2-1 manifold and back to back test them sometime.

I have the logging kit running RPM, Manifold Pressure and Fuel Ratio, this is useful to see exactly where the throttle is and what the mixture is doing. I could use getting the Speed sensor on there also as load and rpm don't always tell you the right picture as more speed = more load!

Reasonably happy with the general performance atm. I made an error in trying to do some logging the other night when it was damp on the road :) I couldn't get any traction over 4800rpm in 3rd, just solid wheelspin to redline....I also had some wheelspin in 4th at 6000rpm...Interesting...2nd was just useless, basically just sit on the spot wheelspinning! It spins the wheels in 2nd at 6000rpm in the dry anyway.

I've been testing quite alot of stuff on a relaxed schedule. I had a persistant pump jet issue and tried 3 types of mechanisms and sorted that...I refuse to use a rolling road to setup the mixture and fuel, so this must be completed by logging and road testing as this translates into the right "feel" for the engine.

Above shows the software I have been using to log AFR, MAP and RPM.

You end up with something like that above...

You can then zoom it. Above shows a moderate acceleration in 4th gear, the MAP reading is high so this indicates an open throttle position in the first 2/3rds of the image. The ideal mixture for peak torque is around 13.2...Here shows I have around 13.2-13.1 during mild acceleration, so perfect. The MAP reading then lowers to 70 as I lift off and start crusing, closing the throttle a bit, the mixture goes to around 14.8-15.0...perfect!

Stoic or perfect combustion is 14.7 (where all fuel and all air is comsumed) and ideal cruise on this engine appears to be 15:1 or so to around 4000rpm. I have some leaner areas in a certain throttle location I will work on, but this is generally how things are at this rpm range.

The image above shows a WOT power-run in 4th. You can see my leanout in the 5700 range. The mixture from there up redline is perfect @ 12.5-12.8. The mixture before the leanout is fine too if you do a long 4th gear run from 3500-7300. I'm not that concerned 13.5 is ok, safe, if it was 14+ I'd be worried.

So I've been busy messing around with this useful info trying to get that best carburettor mix!

I want to sort the rear-end out when the engine is done, cause I will want to go and track the car.

I want to soften the front, down to 330-350lbs springs, it's too hard : 450lbs with an 87kilo engine! Need to sort a hood for it too...

Once that is done the car will be about finished. I'll be looking to sort a better gearbox and some more HP at some point, but no priority atm I want to polish the package first. I'd like to increase the rev limit now from 7300 as the top-end is better but the pistons might give up.

I've no idea how much power it's making. I've not much interest either...It goes fast but you get used to how fast things go don't you :) It's got a few horses anyway cause it was pulling nicely when it hit the limiter in 4th!

I've still not had to put a spanner on any of the work I did and the clutch slave job was perfect!

It's been giving me some decent payback last couple of weeks. However my batteries are still a bit drained. It's better now the engine tuning is coming together and I've got the equipment in to accurately read the dynamics, plus having done quite a few miles in it and nothing appears to be falling apart or suspect. That clutch job pissed me off.

I'd like to move forward from engine fiddling ASAP and start gathering the bits for developing some other areas and just snagging a few bits and sorting a few rattles etc. It was a nice break while I was recalibrating my brain to nicotine free.

I had a gander at the full drama's of the job ~ 2006-2009 on this blog earlier, what a load of work! Christ.

I can feel the "fasting" on working on the car has kindled some motivation I've not made anything or fabricated anything for 2 months, since the clutch job? I think I'll keep it cool for bit longer and work on some easy improvements to keep me hungry. Psychology is important in these big jobs!

Well....

Been a lack of blogging.

No real reason, just been having a quiet period of doing other stuff.

I heard a rumour my car was smashed up, probably started by someone .........We wont go there?!

Well, was fine the other day and unless something fell onto it in the garage? Doubt it.

Well the clutch release fix was top banana. Clutch is 10x lighter can almost push it with your little finger, lightest clutch I have ever had, really smooth, no noise and works really really well. Nice long and progressive bite.

Car has done about 1300miles so far, believe it or not, used it for 2weeks everyday, no problems.

Probably more miles than most of those folks who say my car never leaves the garage :) When it leaves the garage it gets a pounding!

It's currently sat calm while I battle with quiting the fags and getting into shape. Been in a diet of exercise and healthy living. 1month without any smoking. Been pretty easy actually, but had to keep myself to myself and avoid the garage and change my routine. No cars and No Blogging.




I sold my LC-1 Wideband cause I actually sold it for more than I brought it for! So I just waiting to pickup another wideband Lambda unit and finish off the tuning of the engine. To be totally frank I can't seem to crack the jetting, well the last little bit, so I'll have to resort to using technology, I kind of gave up and then quit the fags, thats was a month ago and I've not been near it since. I'd like to get the carbs as good as possible before I make any final judgements on the setup.

I could just about flog the carbs and bits like inlet manifold, fuel pump and stuff and straight swap them to go fuel injected on some jenvey DTH bodies using an Emerald ECU...but first I want to just get the carbs nailed.

I had this sick idea about fitting all the VVC stuff back on, the whole lot and using the stock ECU and plenum...Dunno...like to fiddle, I do like to make sure that i've maxed out what I have got first. Not much work, the wiring would take 10x as long as the cam swap etc.

Top-end could be "bigger" over 6600rpm the cam's might be a bit mild...could use some 285's really...I await my final adjustments first could be a bit rich or lean. Need to test some bigger carb chokes too...Again need a wideband first.

Done alot of messing the cam timing also inlet was good, exhaust needed adjustment as it was unknown....joy of open vernier pullies; i was doing road side adjustments in under 2mins per adjustment!

I made a few videos of it driving...

Oh and rear damper is dead, buggered to replace it atm, I want to ditch the entire rear-end, so awaiting the motive on that, diff's had it too, leaking and the entire lot needs sorting....

It works, I'm relieved at that, the next stages will happen whenever I feel like it...

Kind of glad to be out of the Triumph Engine lark...I built 4 stages/4x 1300 engines from 2001-2006 before the final one in 2006, each more powerful than the previous, I had my fill....I maxed out that cast iron stuff...People still often comment I built one engine, blew it up and fitted something else....That's nonsense.

The previous engine to the grey one of 2006 was the best, cause it lasted AGES took a total beating using the car EVERYDAY doing 250-300miles a week... with motorway trips at 6500-7000rpm in top for 2hrs each way. That engine was great had more torque and only slightly less top-end than the grey one, was easier to tune and ran smoother...The +60 overbore was a mistake on the grey one I reckon, +40 MAX is best. The TH5 and TH7 were crap cams, the previous engines FastRoad89 was much better.

That Grey engine pushed the valves, pistons and everything past what had been a reliable system for me...Basically the extra power and rev's pushed those stock valves past what had been a totally reliable setup...I had been using those types of valves for 4 previous builds, well before I frequented any forums.

The next engine needed to be STEEL and full of expensive parts, to make it reliable, either that or step backwards and detune it...whats the use in going backwards? Sideways or Forwards, but never backwards!

Don't forget, I was messing with those Triumph engines WELL before I setup this blog...I have owned this car for 9 years! I was doing ALOT of miles in it for 4 years. Enough to bash up a set of big-ends every 12months, there's only so much cast iron stuff you can take, and core stock gets worse and harder to find each year.